Background
In my previous post I left out a few things when talking about tranformations. This post is a follow-up on how the camera far plane in Mapbox gl-js is calculated.
Correctly computing the far plane distance ensures that everything is rendered/culled properly (in particular in tilted view).
Let’s far plane
The far plane is affected by the camera’s field of view, its pitch and its altitude, \(r\) (which we already covered in the previous post).
\(\overline{AF}\) is what we are after as seen in the diagram below:
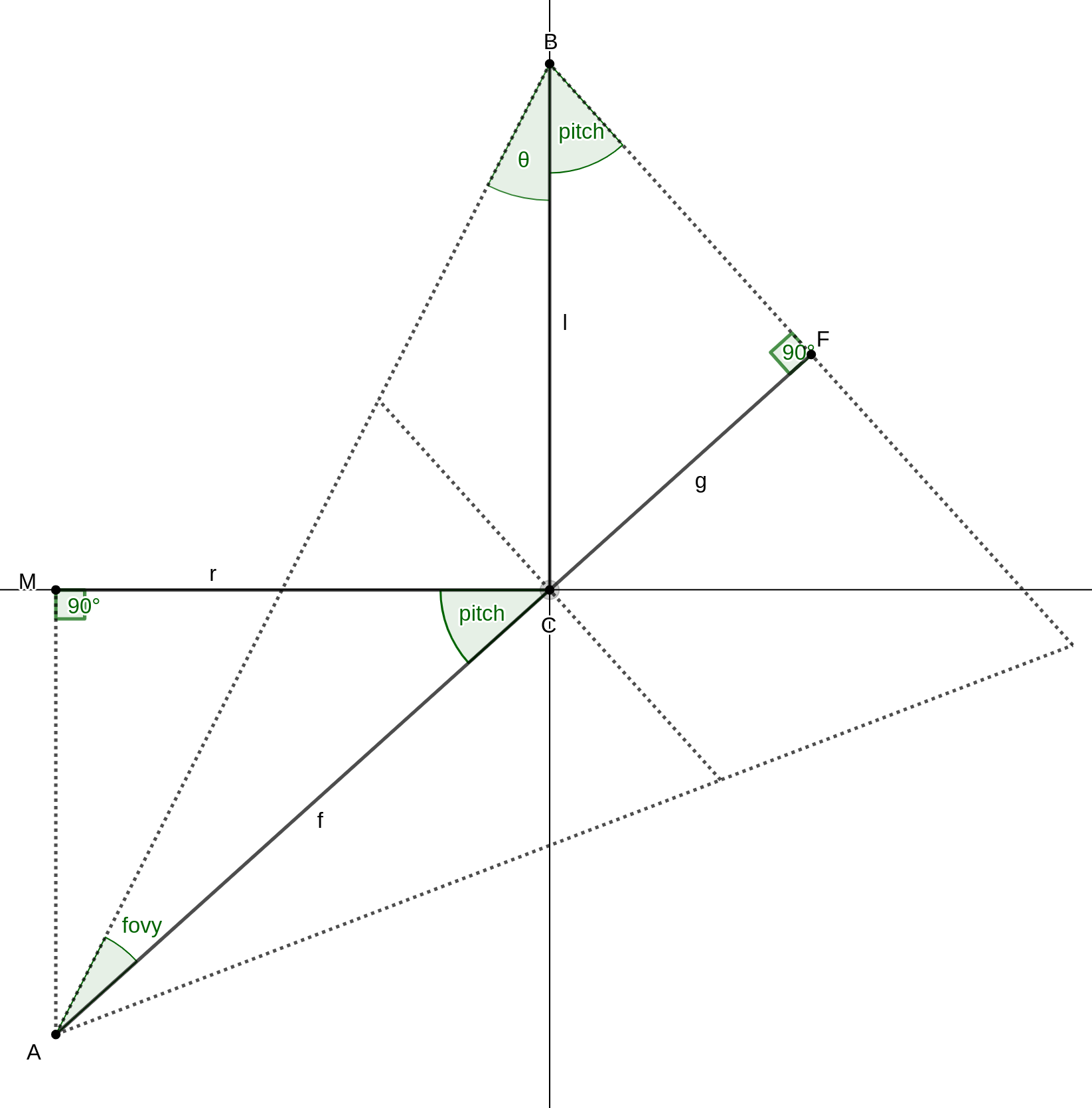
In right-angle \(\triangle{AMC}\) we have:
$$
f = {r \over \cos(pitch)}
$$
From elementary geometry we can deduce that \(\angle{CBF} = pitch\) and \(\theta = {\pi \over 2} - fovy - pitch\).
From law of sines on \(\triangle{ABC}\) we get:
$$ {\sin(fovy) \over l} = {\sin(\theta) \over f} \Rightarrow l = {f \sin(fovy) \over \sin(\theta)} $$
In right-angle \(\triangle{CFB}\) we have: $$ g = l \sin(pitch) $$
This concludes the proof: $$ far\ plane\ distance = \overline{AF} = f + g $$