Background
In his book 3 in the fantastic series Raytracing in a weekend Peter Shirley computes an integral numerically and leaves the analytical solution as an exercise.
This analytical proof is presented below.
Proof
Putting everything down formally, this is what we’re tryign to compute:
$$
\iint_{\Omega} f dS
$$
The integrand is a function in spherical coordinates, that is \(f(r, \theta, \phi) = \cos^2(\theta) \). Domain of integration is denoted by \(\Omega\)
which is the surface of a unit sphere. \(dS\) reprensents an infinitesimally small “patch” over the unit sphere’s surface.
We can describe \(dS\) in terms of \(d\theta\) and \(d\phi\):
$$
dS = \sin(\theta) d\phi d\theta
$$
As seen in the figure below:
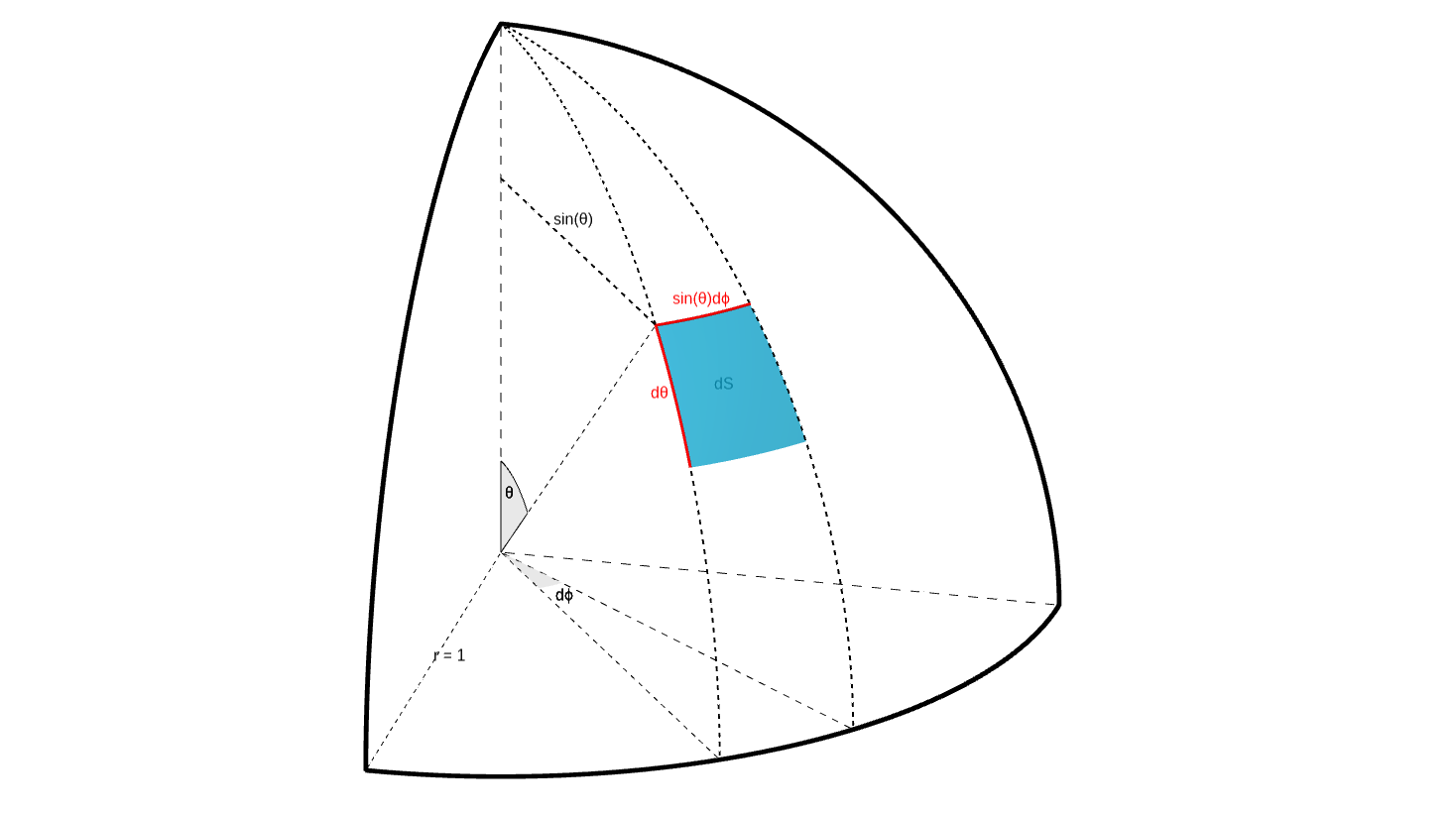
Which you can also see here
Since the sphere is symmetrical we can integrate the first quadrant and multiply the result by 8. Putting everything together:
$$
\begin{aligned}
I &= 8 \int_0^{\pi \over 2} \int_0^{\pi \over 2} cos^2(\theta) \sin(\theta) d\theta d\phi \\ \\
&= 8 \int_0^{\pi \over 2} \Bigg(\small - {1 \over 3} \cos^3(\theta) \Bigg)_0^{\pi \over 2} d\phi \\ \\
&= 8 \Bigg(\small {1 \over 3}\phi \Bigg)_0^{\pi \over 2} = {4 \pi \over 3}
\end{aligned}
$$